The Geographic Grid of Earth System

The Geographic Grid 

It is impossible to lay a flat sheet of paper over a sphere without creasing, folding, or cutting it—as you know if you have tried to gift-wrap a ball. This simple fact has caused mapmakers problems for centuries. Because the Earth’s surface is curved, we cannot divide it into a rectangular grid any more than we could smoothly wrap a globe in a sheet of graph paper. Instead, we divide the Earth into what is known as the geographic grid. This is made up of a system of imaginary circles, called parallels and meridians.

PARALLELS AND MERIDIANS

Imagine cutting the globe just as you might slice an onion to make onion rings. Lay the globe on its side, so that the axis joining the North and South Poles runs perpendicular to your imaginary knife and begin to slice. Each cut creates a circular outline that passes around the surface of the globe. This circle is known as a parallel of latitude, or a parallel. The Earth’s longest parallel of latitude is the Equator, which lies midway between the two poles. We use the Equator as a fundamental reference line for measuring position.

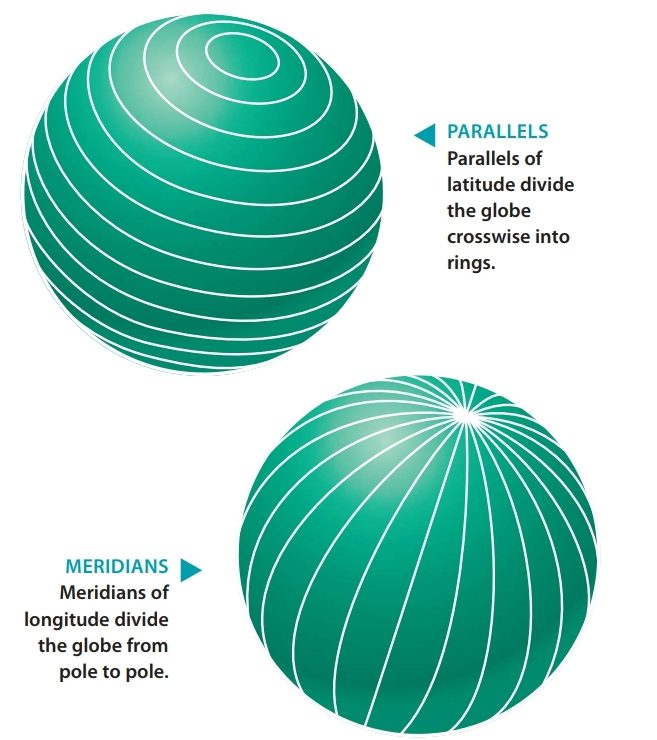
Now imagine slicing the Earth through the axis of rotation instead of across it, just as you would cut up a lemon to produce wedges. The outlines of the cuts form circles on the globe, each of which passes through both poles. Half of this circular outline, connecting one pole to the other, is known as a meridian of longitude, or, more simply, a meridian.

Meridians and parallels define geographic directions. When you walk directly north or south, you follow a meridian; when you walk east or west, you follow a parallel. There are an infinite number of parallels and meridians that can be drawn on the Earth’s surface, just as there are an infinite number of positions on the globe. Every point on the Earth is associated with a unique combi-nation of one parallel and one meridian. The position of the point is defined by their intersection.

Meridians and parallels are made up of two types of circles: great and small. A great circle is created when a plane passing through the center of The Earth intersects the Earth’s surface. It bisects the globe into two equal halves. A small circle is created when a plane passing through the Earth, but not through the Earth’s center, intersects the Earth’s surface. Meridians are actually halves of great circles, while all parallels except the Equator are small circles. Because great circles can be aligned in any direction on the globe, we can always find a great circle that passes through two points on the globe. As we will see shortly, in our discussion of map projections, the portion of the great circle between two points is the shortest distance between them.

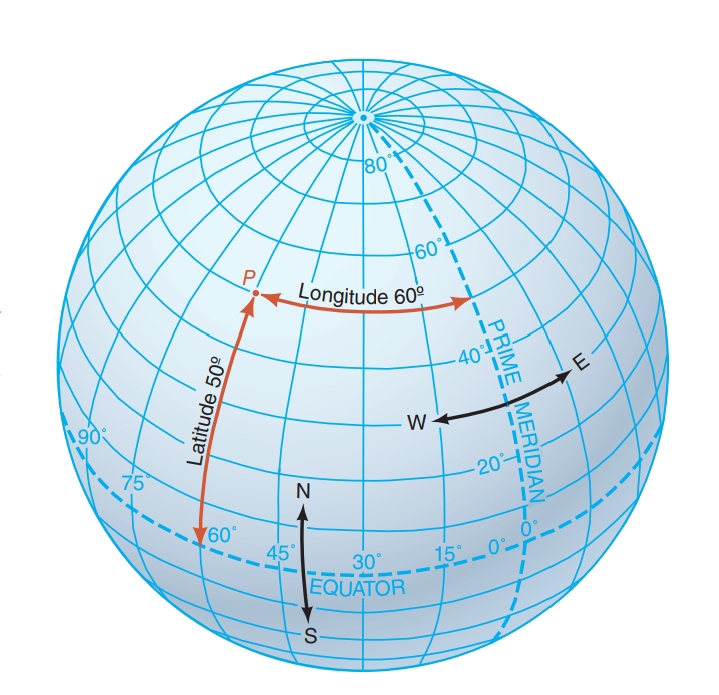
LATITUDE AND LONGITUDE 

We label parallels and merid-ians by their latitude and longitude. The Equator divides the globe into two equal portions: the northern hemisphere and the southern hemisphere. Parallels are identified by their angular distance from the Equator, which ranges from 0° to 90°. All parallels in the northern hemisphere are described by a North latitude (N), and all parallels south of the Equator are given as a south latitude (S). Meridians are identified by longitude, which is an angular measure of how far eastward or westward the meridian is from a reference meridian, called the prime meridian. The prime meridian is sometimes known as the Greenwich meridian because it passes through the old Royal Observatory at Greenwich, near London, England. It has a longitude value of 0°. The longitude of a meridian on the globe is measured eastward or westward from the prime meridian, depending on which direction gives the smaller angle. Longitude then ranges from 0° to 180°, east or west (E or W).

Used together, latitude and longitude pinpoint loca-tions on the geographic grid. Fractions of latitude or longitude angles are described using minutes and seconds. A minute is 1/60 of a degree, and a second is 1/60 of a minute, or 1/3600 of a degree. So, the latitude 41°, 27 minutes (9), and 41 seconds (0) north(lat. 41°279 410 N) means 41° north plus 27/60 of a degree plus 41/3600 of a degree. This cumbersome sys-tem has now largely been replaced by decimal notation. In this example, the latitude 41° 279 410 N translates to 41.4614° N.

Degrees of latitude and longitude can also be used as distance measures. A degree of latitude, which mea-sures distance in a north-south direction, is equal to about 111 km (69 mi). The distance associated with a degree of longitude, however, will be progressively reduced with latitude because meridians converge toward the poles. For example, at 60° latitude, a degree of longitude has a length exactly half of that at the Equator, or 55.5 km (34.5 mi).

A third axis exists for defining locations. Elevation—that is, height or altitude—complements latitude and longitude. Elevation is usually measured from sea level, but can also be expressed as a distance from the Earth’s center. Three-dimensional mapping and analysis rely on the use of elevation to create terrain maps and images that can represent the Earth more realistically.